La probabilidad de que se dé un conjunto \( A \) o \( B \) dado otro conjunto \( C \) viene dada por la expresión

$$P(A + B | C) = P(A | C) + P(B | C) - P(AB | C)$$

se considera que podría ilustrarse con un diagrama de Venn como el de la siguiente figura.

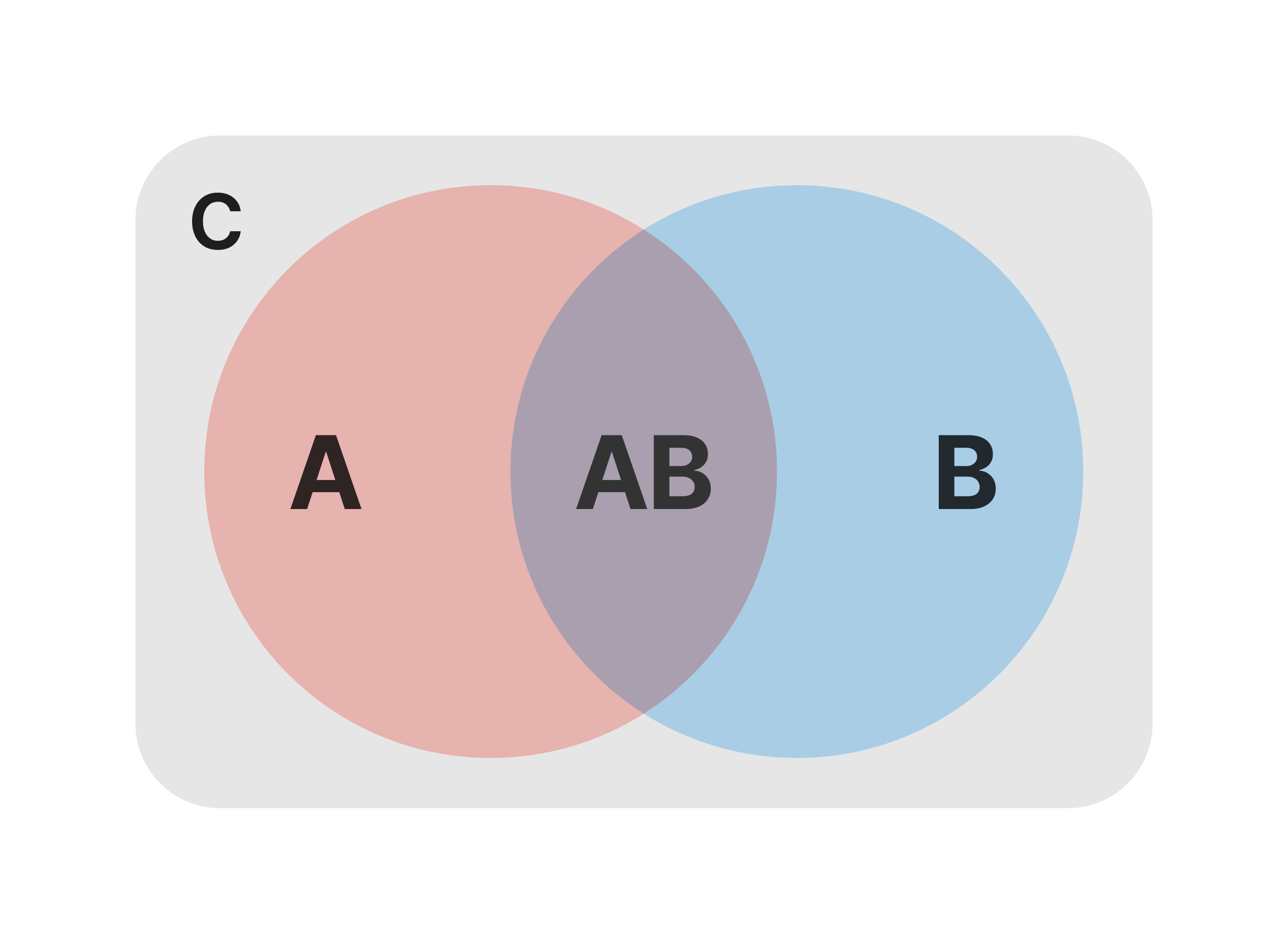
Desde el diagrama, es posible pensar que \(A, B, C\) pueden consistir de infinitos puntos \(\omega_i\) tal que su unión requiere que los puntos de \(A\) y \(B\) se agreguen en un conjunto \(P(A | C) + P(B | C)\), eliminando los puntos que se duplican por estar compartidos entre los dos, o sea \(- P(AB | C)\).

Según Janes, esto es sólo "saltar a la conclusión" de que estas proposiciones son conjuntos con puntos en en espacio. Él propone que \(A, B, C\) son proposiciones lógicas (véanse sus capítulo 1 y 2) en donde la expresión referida se lee traduce en algo parecido a esto: Cuando \(C\) es verdadera, \(A\) o \(B\) son verdaderas, de modo que mientras \(C\) sea verdadera o \(A\) es verdadera, \(P(A | C)\), o lo es \(B\), \(P(B | C)\), pero no los dos a la vez, \(P(AB | C)\).